این پست رو تقدیم می کنم به این مرد خارق العاده
خدمت جناب کورت اشتاینر
با آرزوی بهروزی برای ایشان هر کجا که هستند و خواهند بود
==================================
این پست کمی طولانی است ولی به نظرم ارزش خواندن دارد.
==================================
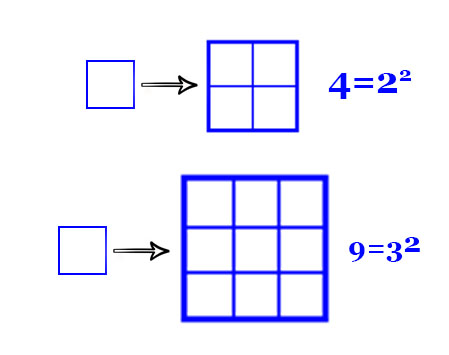
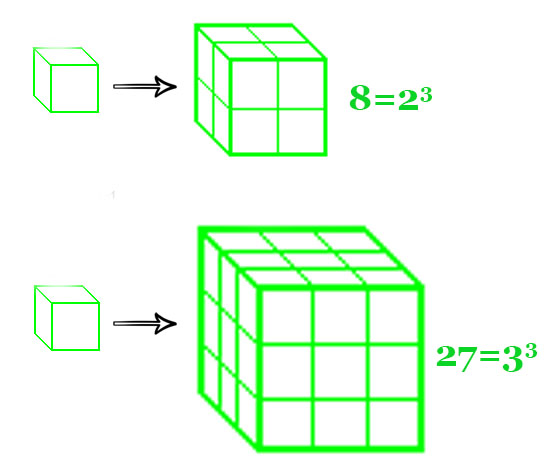
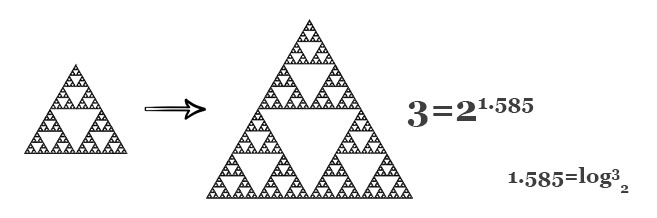
حسن فراکتال ها در مقایسه با سایر مباحث ریاضی این است که اگر از تعریف و ریاضیات پشت آن هم اطلاع نداشته باشید، باز هم می توانید از دیدن آن لذت ببرید، مثل لذتی که از دیدن یک نقاشی یا یک رقص نور می برید...
کل مباحث ریاضی این قسمت از این پست مستحب است و به عنوان مقدمه ای برای بخش بعدی است...
چند سال پیش شخصی به نام سم دربیشایر دست به یک ماجراجویی ریاضی زد. البته قبل این او کسانی کارهای مشابهی انجام داده بودند ولی من بنا به علاقه شخصی ترجیح دادم کار ایشان را در این پست بیاورم. دربیشایر سازنده فایل های GIF صفحات ریاضی ویکی پدیاست که عموما بسیار زیبا و آموزنده هستند...
تصمیم کبری دربیشایر ساختن یک تصویر با کیفیت خیلی بالا از صفحه اعداد مختلط توسط یک ابرکامپیوتر بود. می دانید که صفحه اعداد ماهیتی پیوسته دارد و برای مدل سازی آن در موجود گسسته ای مثل کامپیوتر باید از صفحه نمونه برداری کرد. منظور از تصویر با کیفیت خیلی بالا این است که نمونه برداری ها با فاصله های بسیار بسیار کم انجام شده است. فاصله کم به این معنی است که همه اعداد را با مثلا 20 رقم بعد از اعشار تقریب زده باشیم.
ریاضیات عکس بدین شرح است.
می دانیم چند جمله ای های درجه n در اعداد مختلط دقیقا n ریشه دارد (با احتساب تکرر)
حال تمام چند جمله ای های با درجه کمتر از 25 که ضرایب آن 1+ یا 1- است را در نظر بگیرید. این چند جمله ای ها تعداد زیادی ریشه خواهند داشت. چیزی حدود 400 میلیون عدد مختلط که هر کدام از اعداد دو مولفه با 20 رقم بعد از اعشار دارد...
این محاسبات 4 روز طول کشیده است و حجم داده ای که تولید شده است حدود 5 گیگابایت بوده است. تصور کنید یک فایل txt با حجم 5 گیگابایت پر از عدد!
در واقع این نقاط به شکل نامعلومی درون صفحه پراکنده شده اند. و تا قبل از رسم هیچ ایده ای نداریم که این نقاط کجا هستند.(البته می توان محدوده هایی را مشخص کرد که مسلما نقاط در آنها خواهند افتاد، به عنوان مثال نقاط نمی توانند خیلی از مبدا دور شوند) به نظر باید این نقاط به شکل نامنظمی پخش و پار شده باشند و تصویر نهایی چیزی شبیه صفحه برفکی تلویزیون باشد اما این چنین نیست!
بعد از اتمام محاسبات با یک برنامه مبتنی بر جاوا این نقاط را رنگ آمیزی کرده اند. این رنگ آمیزی بدین گونه است که نقاط سفیدتر حاکی از تراکم بیشتر ریشه ها و نقاط تیره تر نشان گر تراکم کمتر نقاط در آن نواحی است. در نقاط سیاه هم ریشه ای وجود ندارد.
با این مقدمه درباره اینکه معلوم نیست محصول این عکس چه خواهد بود برویم سراغ دیدن عکس. فقط چون دوست نداشتم حین خواندن متن نگاهتون به عکس بخوره لینک دادم!
لینک تصویر:
http://s1.picofile.com/file/8262272218/p..._00_27.jpg
تصویر شگفت انگیزی است و اصلا این چنین به نظر نمی آید که این عکس حاصل رسم ریشه های یک سری معادله با ظاهر ساده باشد. بیشتر شبیه گل و بوته های فرش یا تذهیب ها و نقوش اسلامی است و به نظر کسی با ظرافت خیلی زیادی آن را رسم کرده است...
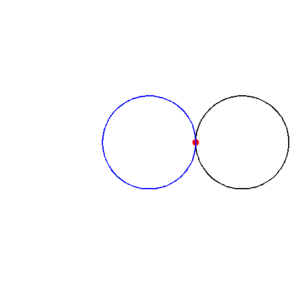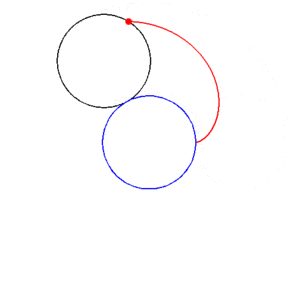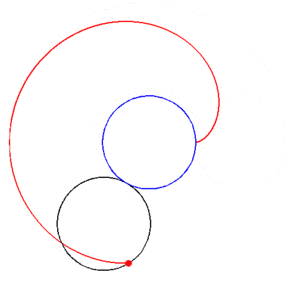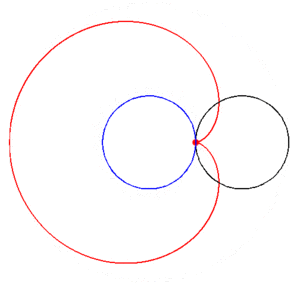
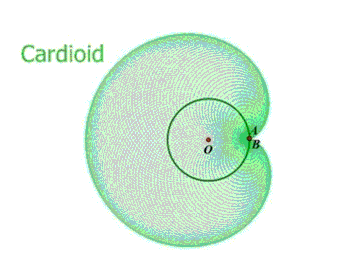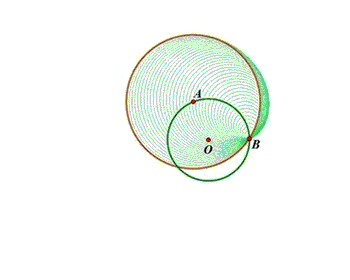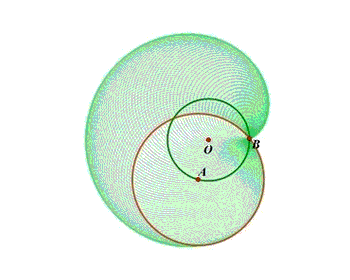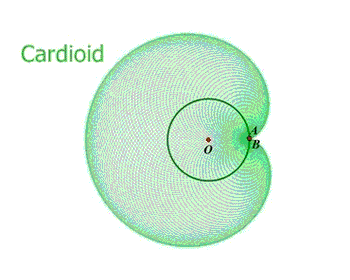
ماجرا وقتی جالب تر می شود که همان فراکتالی که در پست قبل معرفی کردم رو دوباره توی این تصویر ببینید...
http://s1.picofile.com/file/8262272276/p..._00_34.jpg
حالا به این فکر کنید که یک دفعه سر و کله این فراکتال اژدها از کجا پیدا شد؟ ریشه های چندجمله ای رو چه به تا کردن کاغذ؟!!
این جاست که مسئله زیر پیش می آید...
=========================================
آیا ما ریاضیات را کشف می کنیم یا اینکه آن را اختراع می کنیم؟!
این سوال خیلی شبیه اینه که بپرسی آیا خدا وجود دارد یا نه؟
مسلما خیلی ها بدون درنگ جواب می دهند که البته که ما ریاضیات رو کشف می کنیم. چطور ممکنه این همه زیبایی رو یه نفری از خودش درآورده باشه. ولی حداقل چیزی که باید بهش توجه کرد اینه که در تاریخ ریاضیات آدم های زیادی بوده اند که خلاف این رو عقیده داشتند. این آدم ها اصلا هم آدم های خنگ و ساده لوحی نبودند، اتفاقا واقعا آدم های کله گنده ای هم بودند. اعجوبه هایی که به هیچ عنوان نمیشه به میزان نبوغشون حتی فکر هم کرد. البته برعکسش هم بوده. اعجوبه هایی که عقیده داشتند ما ریاضیات رو کشف می کنیم. ولی حداقلش اینه که به احترام اون نوابغ، انقدر سریع و مطمئن نگیم که ریاضیات کشف کردنی است.
به عنوان نمونه یک جمله خیلی کوتاه و صریح از ریاضی دان و فیلسوف معروف ویتگنشتاین میارم: (از کتاب Remarks on the Foundations of Mathematics)
The mathematician is an inventor, not a discoverer

به نظر، شما هم باید موافق نظریه کشفی بودن ریاضیات باشید. حتی اگر تاکنون به این موضوع فکر نکرده بودید با اون عکسی که من آوردم باید معتقد به این نظریه باشید...
در جامعه ما (و خیلی از جوامع مذهبی و غیرمذهبی دیگر) عموما عقیده این گونه است. استدلال هایی که برای تحکیم این نظریه به کار می رود هم عمدتا از جنس مشاهده زیبایی های موجود در ریاضیات، کاربردهای آن در طبیعت و نتیجه گیری دال بر ازلی بودن آن است. با توجه به مظلوم بودن نظریه دوم می خوام در ادامه پست یک کمی از آن دفاع کنم. دفاع نه به این معنی که بگویم نظریه دوم درست است بلکه از این جنس که درست بودن نظریه اول هم چندان واضح نیست و تقریبا هم پای نظریه دوم است...
===========================================
بحث رو از اینجا شروع می کنم. یکی از روش های استدلالی دوستان کشفی(!) این گونه است. یک قضیه خیلی خفن و خوشگل از مثلا هندسه مثال می زنند و می گویند آیا زمانی که اقلیدس داشت کتاب اصول خودش رو می نوشت به مخیله اش هم خطور می کرد که قرار است همچین شاهکاری از آن در بیاید؟ پس اقلیدس که یک انسان ضعیف است این اصول را کشف کرده است نه اینکه خودش آن ها را ساخته باشد...
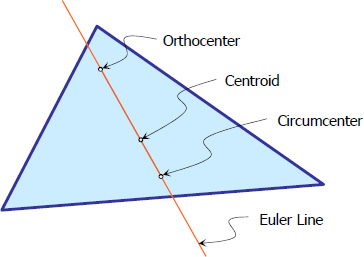
(به عنوان مثال یک مبحثی در هندسه مسطحه هست به نام خط اویلر. می گوید شما هر مثلث دلخواهی را (هر چقدر هم کج و کور!) رسم کنید مرکز دایره محیطی، مرکز ثقل و مرکز ارتفاعیه آن روی یک خط می افتند.البته به مرور زمان کشف شد که فقط همین 3 نقطه نیست بلکه حدود 28 نقطه خاص از هر مثلث، همه روی یک خط قرار دارند و این واقعا شگفت انگیز است... )
در شکل خیلی پیش پاافتاده تر بعضا همچین استدلالی نیز مطرح می شود.
12421433545454557497+325864740349359
می گویند که احتمالا حاصل جمع بالا را تا کنون هیچ کس حساب نکرده است... اگر من بنشینم و این عدد را حساب کنم، آیا به این معنی است که من آن را اختراع کردم، نه مسلما من آنرا کشف کرده ام.
این جمله آخر به نظر استدلال ضعیفی می رسد ولی بنیانش با استدلال مربوط به خط اویلر یکی است!!
باید توجه داشت که اگر در حوزه ای یک چیز جدید و بخصوص یک چیز زیبا پیدا کنیم (کشف کنیم) هیچ دلیلی ندارد که خود آن حوزه یک چیز ازلی باشد.
برای مثال یک بازی را در نظر بگیرید. مثلا بازی حکم! مسلما این بازی نوعی اختراع است. یک شخصی نشسته است و یک سری قوانینی وضع کرده است و این بازی ساخته شده است. (البته اگر از آن دسته آدم هایی هستید که عقیده دارند حکم هم در جایی در عوالم بالا وجود داشته است و آن شخص فقط آنرا کشف کرده است، من دیگه حرفی ندارم!)

این شخص فقط یک سری قوانین گذاشته است. هیچ دلیلی ندارد که این شخص خودش در این بازی مهارت خارق العاده ای داشته باشد یا اینکه از همان روز اول بداند که استراتژی های خوب برای این بازی چیست! احتمالا این شخص در لحظه ای که این قوانین را وضع می کرده است هیچ ایده ای از حرکت هوشمندانه ای مثل تک-بی بی(!) نداشته است. آیا اولین کسی که تک-بی بی کرده است این حرکت را کشف کرده است؟ بله! آیا از این نتیجه می شود که حکم یک بازی ازلی است و از ابتدا بین خدایان چهارگانه رایج بوده است؟! خیر...
اما یک مثال خیلی بهتر. در سال 1970 یک ریاضیدان انگلیسی به اسم جان کانوی یک بازی فلسفی یک نفره (صفر نفره) به نام بازی زندگی را اختراع کرد. صفر نفره از این جهت که شما فقط اول بازی یک چیزی را تعیین می کنید و در بقیه بازی فقط نظاره گر آنچه رخ می دهد هستید. بازی از یک جدول خیلی بزرگ تشکیل شده است که برخی از خانه های آن روشن است. (یا به تعبیری زنده است.)

جان کانوی از جمله آدم هایی است که نبوغ فوق العاده شان از چهره، نگاه و طرز حرف زدنشان کاملا مشخص است...
.
در هر مرحله طی چهار قانون مشخص بعضی از خانه های جدول روشن می شود و برخی دیگر خاموش. در واقع تنها حرکت شما در ابتدای بازی این است که مشخص کنید در اول کار، چه خانه هایی روشن و چه خانه هایی خاموش است. چهار قانون از این قرار است:
1) هر خانه زنده ای که کمتر از دو همسایه زنده داشته باشد، در مرحله بعد (نسل بعد) می میرد.
2) هر خانه زنده ای که بیش از 3 همسایه زنده داشته باشد، در نسل بعد می میرد.
3) هر خانه زنده ای که 2 یا 3 همسایه زنده داشته باشد، در نسل بعد هم زنده می ماند.
4) هر خانه مرده ای که دقیقا 3 همسایه زنده داشته باشد، زنده می شود.
همین!
با همین چهار قانون و حرکت اول بازی شما، این خانه ها زنده و مرده می شوند و به نوعی در طول زمان نسل های مختلفی را تجربه می کنند...
به عنوان مثال اگر شما در حرکت اول دو مربع 2*2 که یک راس مشترک دارند را رسم کنید در طول زمان اتفاق زیر می افتد.

دو خانه گوشه چون چهار همسایه زنده دارند می میرند ولی در نسل بعد چون همین دو خانه مرده، دقیقا سه همسایه زنده دارند، زنده می شوند و این اتفاقا مکررا خواهد افتاد.
این بازی رو می تونید از اینجا ببینید:
http://pmav.eu/stuff/javascript-game-of-life-v3.1.1
توصیه هم می کنم قبل از خوندن ادامه متن حداقل یک بار بازی کنید. نسبتا مفرحه که ببینید چه بلایی سر اولین نسلی که تولید کردید میاد. ممکنه منقرض بشه، ممکنه ثابت بشه یا توی لوپ بیفته. ممکن هم هست هی اتفاقات جدید بیفته. خلاصه لذتی خدای گونه دارد! (به قول هانا اشمیت گرامی)
حالا با همین 4 تا قانون ساده که جناب کانوی ابداع کرده است آیا می توان چیزهای زیبا و خارق العاده ای کشف کرد؟ بعلاوه اینکه اگر ما چنین چیزهایی را کشف کنیم آیا دلیل می شود که این بازی کانوی یک چیز ازلی باشد؟

GIF بالا از صفحه ویکی پدیای بازی زندگی برداشته شده است که نسبتا شکل زیبا و جذابی است اما برای اینکه ببینید چقدر مخلوقات فوق العاده ای می توان با این قوانین ساده به وجود آورد ویدئوی زیر را مشاهده کنید. این ویدئو تنها با استفاده از آهنگ زیبای فیلم مرثیه ای برای یک رویا، کل چیزی که سعی دارم در این پست بگم رو خیلی بهتر و سینمایی تر گفته است... آیا خود کانوی می دانست که چنین چیزهایی به وجود خواهند آمد؟
البته دقت کنید که این استدلال ثابت نمی کند که ریاضیات اختراع بشر است ولی در اینکه ریاضیات یک چیز ازلی است شک ایجاد می کند...
======================================
استدلال دیگری که برای ازلی بودن ریاضیات به کار می رود کاری با زیبایی ندارد. در واقع با کاربردی بودن آن کار دارد. به این معنی که می گوید قوانین طبیعت، مثل قانون جاذبه را ازلی حساب می کنیم. پس ریاضیاتی که برای توصیف آن به کار می رود و جواب هم میدهد ازلی است.
البته این استدلال هم کمی جوب دارد. به این دلیل که چه لزومی دارد ابزاری که برای حل یک مشکل به کار می رود مثل آن باشد. درست است که قوانین فیزیکی ازلی هستند ولی ممکن است این فرمول ها و ریاضیاتی که ما برای تقریب آن ها استفاده می کنیم ابداعی باشد.
دقت کنید که تعداد زیادی از فیزیک دانان معتقدند که کل جهان گسسته است. در واقع همه چیز از جمله حرکات و راه رفتن ما هم گسسته است ولی با استپ هایی در اندازه زیر اتمی. حال در این صورت وجود حساب دیفرانسیل و انتگرال که در آن همه چیز حالت گسسته دارد چه معنایی می دهد؟ وقتی در دنیای واقعی دو چیز از یک حدی نمی توانند به هم نزدیک بشوند چطور از میل کردن یک متغیر به یک عدد صحبت می کنیم. میل کردنی که در آن می توانند به دلخواه به هم نزدیک شوند؟ به نظر می رسد در حالیکه حساب دیفرانسیل به شکل وسیعی در فیزیک دنیا کاربرد دارد ولی مبنایی در دنیا ندارد و صرفا یک اختراع است...
این چنین به نظر می رسد که ریاضیات فقط یک زبان است برای توصیف دنیا. همانطور که زبان فارسی یک ابزار است برای توصیف تفکرات ما... دقت کنید که یک بسکتبالیست (و اگر اساعه ادب نشود، در حالت خیلی افراطی تر یک سگ) برای فهمیدن محل فرود توپ به هیچ عنوان از ریاضیات استفاده نمی کند. حتی در ذهن او نیز کوچک ترین اثری از ریاضیات عبور نمی کند. ولی خیلی بهتر از فرمول های پیچیده ریاضی، با وجود مزاحمت های نیروی مقاومت هوا و ... می تواند بخوبی آن را پیش بینی کند. به نظر او از ابزاری بهتر از ریاضی استفاده می کند.

یک پرانتز: ( یکی از چیزهایی که بارها شنیده ایم این است که نور ماهیتی دوگانه دارد. بعضی اوقات به شکل انرژی است و بعضی اوقات به شکل ماده. این دقیقا من رو یاد فعلی مثل Get می اندازد که در ترجمه آن به زبان فارسی در برخی موارد معنای گرفتن می دهد و برخی موارد معنای رسیدن و ... یک طرز فکر بامزه این است که اینجوری به این مشکل فیزیکی نگاه کنیم که زبانی که ما برای توصیف طبیعت انتخاب کرده ایم با زبان اصلی آن فرق دارد!)
یک مثال هم از ترکیب دو استدلال فوق (تقدیم مجدد به جناب کورت که اهل شعر هم هستند) :
سمن بویان، غبار غم، چو بنشینند بنشانند پری رویان، قرار از دل، چو بستیزند بستانند
واقعا این شاهکار حافظ در زیبایی چیزی کم از فراکتال مندلبروت ندارد. وقتی زبان فارسی در طول زمان ساخته می شد (اختراع میشد) چه کسی فکرش را می کرد که با کنار هم گذاشتن چند کلمه ساده همچین شعری بوجود بیاید... آیا اینکه این شعر انقدر زیباست دلیل این می شود که خدایان به زبان فارسی صحبت می کنند؟!
توجه داشته باشید این مثال کمی از مثال های قبلی افراطی تر است.
در مثال های قبل اصول را با لفظ اختراع می آوردم و قضایا و چیزهای زیبا و جالب را با لفظ کشف.
ولی درمورد شعر حافظ نه تنها اصول (که همان زبان فارسی است) اختراع است بلکه شعر زیبای حافظ هم به نوعی اختراع است.
=========================================
در ریاضیات علاوه بر هندسه مسطحه که در مدرسه با آن آشنا شدیم، هندسه های دیگری هم هست. یکی از آن ها هندسه کروی است. در هندسه کروی معنای خط چیز دیگری است. خط ها همان دایره های عظیمه کره خواهند بود، مثل استوا و نصف النهار ها. (دقت کنید که مدارها (دایره های کوچک تری که موازی با استوا رسم می شوند) خط محسوب نمی شوند.)
در هندسه کروی دیگر خطوط موازی معنا ندارد. چون هر دو خطی (هر دو دایره عظیمه ای) که روی کره است دقیقا در دو نقطه همدیگر را قطع می کنند. (مثل نصف النهار ها که در دو قطب همدیگر را قطع می کنند)
ما دو هندسه مختلف را تا اینجا شناختیم و تعداد خیلی زیاد دیگری هم هست که از حوصله این پست خارج است. این دو هندسه مختلف حاصل تعدادی (پنج تا) اصل است که ابتدای کار ما این اصول را پذیرفته ایم. (چون باید بالاخره یک چیزی را مبنا گرفت و نمی توان هر قضیه ای را به یک قضیه دیگر ارجاع داد چراکه در دور می افتیم.)
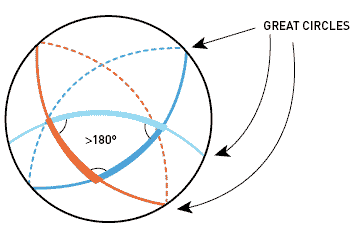
صحبت اصلی یک جورایی بر سر این است که این پنج اصل از کجا آمده است؟ آیا اقلیدس آن ها را اختراع کرده است یا کشف کرده است. مسلما جواب را خود اقلیدس هم نمی داند. ولی آیا اگر آن زمان، اقلیدس می دانست که زمین گرد است آیا باز هم همین اصول را می نوشت؟!
از هندسه که بگذریم، نظریه اعداد هم بحث خودش را دارد...
اگر ریاضی دانی وجود نداشت آیا اعداد وجود داشتند؟ (به نظر جواب مثبت است.)
اعداد اول چطور؟ چرا اعداد اول هیچ فرمولی محاسبانی ندارد؟
اعداد منفی چطور؟ آیا اعداد منفی یک اختراع و قرارداد برای سهولت محاسبات نیست؟
اعداد مختلط چطور؟! آن هم اعداد مختلطی که اشکالی مثل همان نقش قالی را می سازند و در فرمول های الکترومغناطیس ظاهر می شوند. با این حال حقیقی نیستند و در دنیای ما وجود ندارند!
شاید این جمله ریاضی دان معروف لئوپولد کرونکر را شنیده باشید:
خداوند اعداد صحیح را خلق کرد؛ همه چیزهای دیگر کار انسان است!
==========================================

خلاصه اینکه خیلی معلوم نیست که ریاضی دان ها دقیقا دارند چه می کنند!
مثل یک باستان شناس در پی کشف چیزهای پنهانند؟ (دیدگاه کشف ریاضیات)
مثل یک مهندس ماجراجو در حال ساختن کشتی ای هستند که بتوانند با آن در دریای حقیقت به اکتشاف بپردازند. (دیدگاه اختراع اصول موضوعه ولی کشف قضایا)
یا مثل یک مهندس سرخوش در حال ساختن Lego های مختلف اند تا با آن چیزهای جالب بسازند! (دیدگاه اختراع اصول موضوعه و اختراع قضایا)
ولی چیزی که هست اینکه صحبت در این باره بیش از هرچیز آدم رو یاد این شاهکار سینمایی می اندازه...

===============================================
در ورای این نظریه ها یک نظریه دیگری به اسم !Shut Up & Calculate می گوید هیچ اهمیتی ندارد که ریشه ریاضیات چیست و فقط لذت بردن و استفاده کردن از آن مهم است.
به نظر دیدگاه منطقی است ولی دقت کنید هرچند دیدگاه کشفی بودن ریاضیات در قدیم منجر به پرداخت و پیشرفت آن شده است ولی در خیلی از موارد مضر بوده است. نمی گویم اگر اعتقاد داشته باشیم ریاضیات اختراع شدنی است جنگ و خون ریزی کمتری در دنیا خواهیم داشت ولی اگر کسی این گونه به ریاضیات نگاه کند به نظر باید شجاع تر و ماجراجو تر باشد. به نظر با آرامش خاطر دیگری دست به گشت و گذار در این عالم میزند و با ترس کمتری ایده های عجیب و غریب خودش را دنبال می کند. چرا که می داند خودش هست و خودش. این اوست که باید تعاریف و قضایای جدیدی را بسازد. و این محصولات او باید به اندازه کافی زیبا و سازگار باشد که در طول تاریخ دچار بلای انتخاب طبیعی نشود...
ضمن اینکه در تاریخ ریاضیات هم اتفاقات قابل تاملی افتاده است.
بعد از فیثاغورث یک مکتب فیثاغورثی پدیدار شده که تقریبا به شکل دین درآمده بوده است. آن ها عقیده داشته اند که همه اعداد گویا هستند و وقتی هیپاسوس برای اولین بار ثابت کرد که طول قطر یک پنج ضلعی منتظم عددی گنگ است او را کشتند!

این تعصب صرفا از این جهت به وجود آمده بوده است که اهالی این مکتب عقیده داشتند که ریاضیات یک چیز ازلی است و برای آنها قابل باور نبوده است که عددی پیدا شود که نتوان آن را به شکل یک نسبت نوشت. شاید اگر این عقیده نبود ریاضیات زودتر پیشرفت می کرد و ریاضیات عمیق تری به ما می رسید. شاید اگر این عقیده نبود 2000 سال وقت ریاضی دانان صرف اثبات اصل پنجم اقلیدس از روی چهار اصل دیگر نمی شد. شاید گاوس مجبور نبود به پایه های هندسه نااقلیدسی بپردازد و می توانست چیزهای خارق العاده تری کشف کند.
البته ممکن است بعضی ها بگویند:
حالا مثلا اگه ریاضیات پیشرفته تر می شد چه اتفاق خاصی می افتاد؟ چه تغییری به حال ما می کرد؟ مگه چند نفر کل کارهای خارق العاده گاوس رو فهمیدن که حالا نگران باشیم که ای کاش این کارها بیشتر می بود؟ کسانی که 2000 سال وقتشون رو صرف همچین چیز مسخره ای کردند، حقشون بوده که به این حماقت ادامه دهند...
در جواب باید گفت به نظر این عقیده آن ها کاملا درست است! به نظر اهمیتی ندارد که ریاضی و فیزیک چقدر پیشرفت کند. تکنولوژی به کجا برسد. فرقی ندارد برق تولید شده باشد یا نه. حتی اهمیتی ندارد که ما همچنان در غار زندگی می کردیم یا نه. به نظر چیزهای مهم تری هم باید وجود داشته باشد ولی متاسفانه وجود ندارد.
----------------
لینک تصویر ریشه های چندجمله ای ها با کیفیت اصلی و حجم 90 مگابایت!
http://www.math.ucr.edu/home/baez/roots/..._roots.png
![[-]](images/collapse.gif)
 پيام :
پيام :

 تشکر شده توسط :
تشکر شده توسط :



 تشکر شده توسط :
تشکر شده توسط :



 تشکر شده توسط :
تشکر شده توسط :



 تشکر شده توسط :
تشکر شده توسط :



 تشکر شده توسط :
تشکر شده توسط :



 تشکر شده توسط :
تشکر شده توسط :



 تشکر شده توسط :
تشکر شده توسط :



 تشکر شده توسط :
تشکر شده توسط :



 تشکر شده توسط :
تشکر شده توسط :



 تشکر شده توسط :
تشکر شده توسط :
 جست و جو
جست و جو لیست کاربران
لیست کاربران تقویم
تقویم راهنمایی
راهنمایی